Craps Odds Explained in Detail

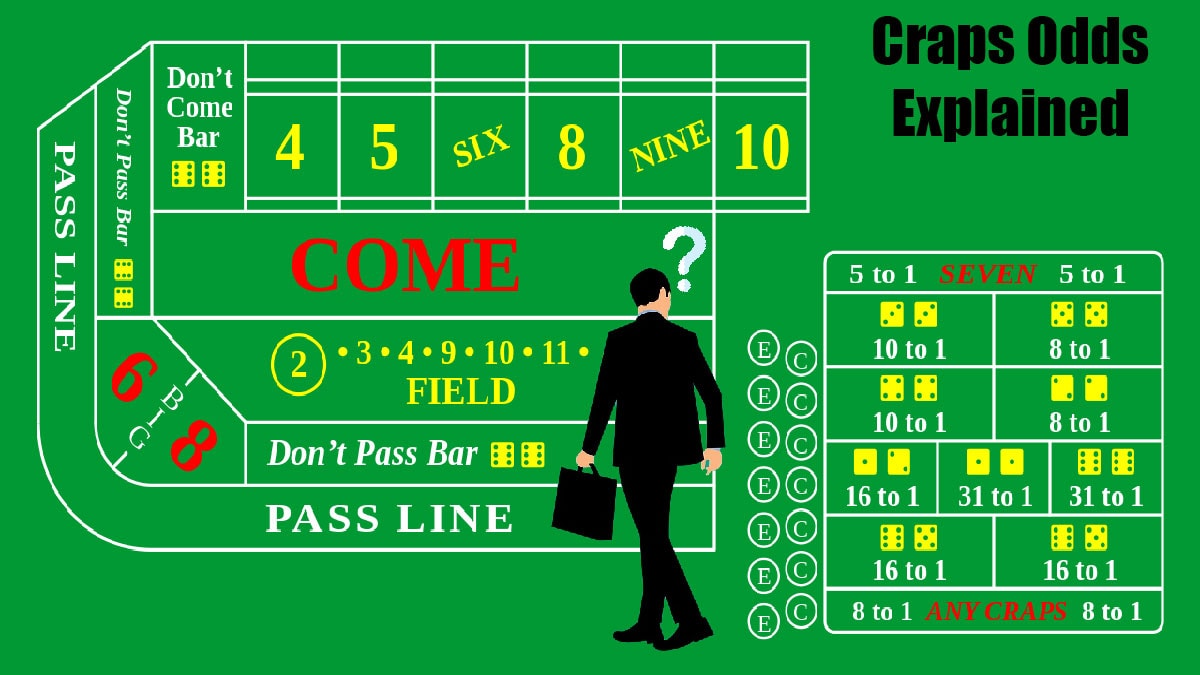
The title of this post is “Craps Odds Explained in Detail,” and that’s exactly what I plan to do in this post: explain craps odds in details. This will, naturally, include an answer to the question, “What is the best bet in craps?”

It will also include some thoughts on the odds of winning at craps compared to the odds of losing. I also have some thoughts on the subject of consistently winning at craps, we will get into that as well.

General Probability and Craps-Specific Probability

Explaining craps odds necessitates understanding some basics of probability.

Probability is just a mathematical explanation of the likelihood that something will happen. When you talk about the odds of something happening, you’re describing its probability.

When I roll a six-sided die, the probability of getting a 1 is 1/6. There are 6 possible outcomes, but only one of them is a 1.

If I want to express that as odds, I compare the number of ways that it can’t happen with the number of ways it can.

The odds of rolling a 1 are 5 to 1. (You have 5 outcomes that aren’t a 1, compared with one outcome that is a 1.”

When you roll a pair of six-sided dice, like you do in craps, you have 36 possible outcomes and 11 possible totals:

• 1 way to roll a 2.
• 2 ways to roll a 3.
• 3 ways to roll a 4.
• 4 ways to roll a 5.
• 5 ways to roll a 6.
• 6 ways to roll a 7.
• 5 ways to roll an 8.
• 4 ways to roll a 9.
• 3 ways to roll a 10.
• 2 ways to roll an 11.
• 1 way to roll a 12.

If you want to know the odds of rolling a 7, the math is simple – you have 6 ways out of a possible 36 outcomes, which is 6/36.

As with any fraction, you can reduce that to 1/6, which means the odds of rolling a total of 7 are 5 to 1.

This is the beginning of understanding craps odds.

Things to Understand about Probability

Here are a couple of other things to understand about probability:

• If you add the probability of something happening with the probability of it not happening, the total is always 100%.
• If you want to know the probability that one of multiple events are going to happen, you just add them up.

For example, what if you want to know the odds of getting a 7 OR an 11 on a roll of the dice?

You have 2 ways to roll an 11, and you have 6 ways to roll a 7, so you have 8 ways out of 36 possible outcomes that will result in a 7 or an 11.

That’s 8/36, or 2/9, which comes out to 7 to 2 odds, or 3.5 to 1.

That’s 5 possible outcomes out of 36, which means the odds are 31 to 5. That’s about 7.2 to 1.

What are the odds of getting any other total besides 2, 3, 7, 11, or 12?

You have 24 ways of rolling something else, compared to 12 ways of rolling those totals. That’s 12/36, or 1/3, or 2 to 1 odds.

When you roll the dice on a come-out roll in craps, you have 3 possibilities:

• An immediate success (7 or 11)
• An immediate failure (2, 3, or 12)
• A point (any other number)

2 out of 3 times, you’ll see a point rolled.

The rest of the time, the outcome will be determined immediately.

How the House Gets Its Edge in Craps (And Other Games)

The house gets is edge in craps the same way it does in other games: it pays off bets at odds that are lower than the odds of winning.

Let’s suppose you’re able to bet on the come-out roll that you’re going to see a resolution immediately. (We’ll call it the immediate resolution bet.)

And let’s assume that this bet pays off at even money. If the odds hold true, which they tend to do over the long run, the house will win your money fast.

Over 3 rolls, you’ll win once and lose twice. That’s $100 in winnings versus $200 in losses. Your net loss is $100.

Average that out over 3 rolls, and you’ve lost an average of $33.33 per roll of the dice. That’s 33.33% of your stake, which is the house edge on that bet.

Luckily, that bet’s not available at the craps table, but that’s how the logic and math behind all the bets work.

What Is the Best Bet in Craps and Why?

The best bet in craps, from a pure examination of the odds, is the odds bet. It pays off at the same odds you have of winning.

The odds bet is a bet you’re only able to place AFTER the come-out roll and a point has been set. If the come-out roll is resolved immediately, you can’t place this bet. Also, you must have already placed a pass or don’t pass bet to make an odds bet.

What are the odds of rolling a 4, for example? You have 3 ways to roll a 4, versus 6 ways to roll a 7.

This means that the odds of rolling a 4 before rolling a 7 are 6 to 3, which reduces to 2 to 1.

And guess what the payout is for this bet? It’s 2 to 1.

That holds true for the other point totals.

The house edge on the odds bet is the only 0% in the house.

The problem is that you can’t place this bet unless you’ve already placed a pass line or don’t pass line bet.

Which Bets Should You Make?

Since you can’t place the odds bet in isolation, the best bets at the craps table are the most basic bets – the pass line bet and the don’t pass bet.

I’m not going to run through all the math involved in getting there, but take my word for it:

• The house edge for the pass line bet is 1.41%.
• The house edge for the don’t pass bet is 1.36%.

That’s a minimal difference, but if you care about such things, you should go with the don’t pass bet.

If you combine this with the odds bet, the house edge on the cumulative amount of money drops considerably.

The come bet and the don’t come bet have the same house edge figures as the pass and don’t pass bets. The only difference is that the come and don’t come bets treat the next roll as a come-out roll, regardless of where you’re at in the action.

Those are really the only bets worth making at the craps table.

The house edge skyrockets on the other bets.

Can You Consistently Win at Craps?

That’s a legitimate question. The short answer is no, because dice rolls are random, and the odds of winning are always worse than the payout odds.

But what if you could control (or even influence) the probability of the outcomes?

With a house edge that low, if you could set the dice before throwing them in such a way that they were less likely to land on 7 when you’re trying to roll the point, could you theoretically shift the odds in your favor so that you’ll have an edge? Theoretically, yes.

Practically, though? I don’t know anyone who’s demonstrated mathematically that dice control is a real possibility.

I’ve read legitimate gambling writers suggest that it’s possible, though.

Conclusion

I love writing about craps, and I hope this “craps odds explained” post sheds some light on the math behind the game for you.

If nothing else, you should come away from this post with a clear understanding of what is the best bet in craps.

I wish I had a more definitive answer to offer on whether you can consistently win at craps, but I don’t.

• Updated Super Bowl 59 Odds: Which Teams Improved in the Draft?
• The Best Egyptian Slots to Play Online
• WWE Backlash France Odds and Expert Picks

• Updated Super Bowl 59 Odds: Which Teams Improved in the Draft?
• The Best Egyptian Slots to Play Online
• New Online Slots to Play This Month